韭零后

公元1996 - ?

0%

DOUBLESQUEEZE Parallel Stochastic Gradient Descent with Double-pass Error-Compensated Compression

发表于 更新于 分类于 ， ， ， 阅读次数： Valine：
本文字数： 9.1k 阅读时长 ≈ 8 分钟

摘要

目前已有类似于QSGD和稀疏化SGD的通信优化算法，但参数服务器在实际应用中在收到工作节点量化梯度并聚合后，需要将聚合梯度从新分发给工作节点。本论文同时对工作节点和参数服务器梯度，采用误差补偿的方式进行梯度压缩。该算法有三大优势：

  1. 它兼容众多“粗暴”的压缩技术
  2. 它与没有误差补偿的压缩算法（例如QSGD和稀疏化SGD）相比，收敛性更好
  3. 达到了线性收敛
1
2
if __name__ == "__main__":
    print("111")

dfdfadf

背景介绍

提高分布式机器学习性能的三个方向：

（1）高通信效率的学习

  • QSGD: Communication-efficient SGD via gradient quantization and encoding1（量化为三元组表示）
  • signSGD: Compressed optimisation for non-convex problems2
  • 1-bit stochastic gradient descent and its application to data-parallel distributed training of speech dnns3（提出一种误差补偿的量化方法）

（2）去中心化学习；

  • He L, Bian A, Jaggi M. Cola: Decentralized linear learning[C]//Advances in Neural Information Processing Systems. 2018: 4536-4546.
  • Lian X, Zhang C, Zhang H, et al. Can decentralized algorithms outperform centralized algorithms? a case study for decentralized parallel stochastic gradient descent[C]//Advances in Neural Information Processing Systems. 2017: 5330-5340.

（3）异步学习

  • Agarwal A, Duchi J C. Distributed delayed stochastic optimization[C]//Advances in Neural Information Processing Systems. 2011: 873-881.
  • Lian X, Huang Y, Li Y, et al. Asynchronous parallel stochastic gradient for nonconvex optimization[C]//Advances in Neural Information Processing Systems. 2015: 2737-2745.
  • Recht B, Re C, Wright S, et al. Hogwild: A lock-free approach to parallelizing stochastic gradient descent[C]//Advances in neural information processing systems. 2011: 693-701.

量化压缩基本模型

作者对分布式机器学习（特别是参数服务器架构）和量化压缩数学模型简单做了介绍

分布式机器学习基本模型

\[ \min _{\boldsymbol{x}} f(\boldsymbol{x})=\frac{1}{n} \sum_{i=1}^{n} \mathbb{E}_{\boldsymbol{\zeta} \sim \mathcal{D}_{i}} F(\boldsymbol{x} ; \boldsymbol{\zeta}) \]

其中\(n\)表示工作节点数量，\(\mathcal{D}_{i}\)本地节点\(i\)的数据分布，\(F(\boldsymbol{x} ; \boldsymbol{\zeta})\)为本地损失函数。 \[ \boldsymbol{g}^{(i)}=\nabla F\left(\boldsymbol{x} ; \boldsymbol{\zeta}^{(i)}\right) \] 各工作节点计算梯度 \[ \boldsymbol{g}=\frac{1}{n} \sum_{i=1}^{n} \boldsymbol{g}^{(i)} \] 参数服务器对梯度进行聚合，以上是对分布式SGD算法的简单建模

量化压缩

\(Q_{\omega}[\cdot]\)代表压缩操作，以\(1Bits\)方法为例，利用递归的方法更新压缩误差： \[ \boldsymbol{\delta}^{(i)}=\boldsymbol{g}^{(i)}+\boldsymbol{\delta}^{(i)}-Q_{\omega}\left[\boldsymbol{g}^{(i)}+\boldsymbol{\delta}^{(i)}\right] \] 其中\(\left[\boldsymbol{g}^{(i)}+\boldsymbol{\delta}^{(i)}\right]\)表示本轮计算得到的梯度\(g^{(i)}\)和上一轮压缩误差\(\boldsymbol{\delta}^{(i)}\)的和，上式子是对本轮量化误差的重新计算，这也是误差补偿的由来。

主要贡献

  1. 比其他没有错误补偿的压缩方法具有更好的收敛性
  2. 进一步优化了通信效率
  3. 第一次给出了误差补偿SGD相关算法的速率分析
  4. 在非凸情况下的加速证明

相关工作

分布式学习

中心化并行训练
参数服务器架构
  1. Abadi M, Barham P, Chen J, et al. Tensorflow: A system for large-scale machine learning[C]//12th {USENIX} symposium on operating systems design and implementation ({OSDI} 16). 2016: 265-283.
  2. Li M, Andersen D G, Park J W, et al. Scaling distributed machine learning with the parameter server[C]//11th {USENIX} Symposium on Operating Systems Design and Implementation ({OSDI} 14). 2014: 583-598.
去中心化训练
  1. 固定拓扑
    • Jin P H, Yuan Q, Iandola F, et al. How to scale distributed deep learning?[J]. arXiv preprint arXiv:1611.04581, 2016.
    • Lian X, Zhang C, Zhang H, et al. Can decentralized algorithms outperform centralized algorithms? a case study for decentralized parallel stochastic gradient descent[C]//Advances in Neural Information Processing Systems. 2017: 5330-5340.
    • Shen Z, Mokhtari A, Zhou T, et al. Towards more efficient stochastic decentralized learning: Faster convergence and sparse communication[J]. arXiv preprint arXiv:1805.09969, 2018.
    • Tang H, Lian X, Yan M, et al. D \(^ 2\): Decentralized Training over Decentralized Data[J]. arXiv preprint arXiv:1803.07068, 2018.
  2. 随机拓扑
    • Lian X, Zhang W, Zhang C, et al. Asynchronous decentralized parallel stochastic gradient descent[C]//International Conference on Machine Learning. 2018: 3043-3052.
    • Nedić A, Olshevsky A. Distributed optimization over time-varying directed graphs[J]. IEEE Transactions on Automatic Control, 2014, 60(3): 601-615.
    • Nedic A, Olshevsky A, Shi W. Achieving geometric convergence for distributed optimization over time-varying graphs[J]. SIAM Journal on Optimization, 2017, 27(4): 2597-2633.
不同角度实现分布式训练
  1. 隐私分布式优化
    • Jayaraman B, Wang L, Evans D, et al. Distributed learning without distress: Privacy-preserving empirical risk minimization[C]//Advances in Neural Information Processing Systems. 2018: 6343-6354.
  2. 自适应分布式ADMM
    • Xu Z, Taylor G, Li H, et al. Adaptive consensus ADMM for distributed optimization[J]. arXiv preprint arXiv:1706.02869, 2017.
  3. 非平滑分布式优化
    • Scaman K, Bach F, Bubeck S, et al. Optimal algorithms for non-smooth distributed optimization in networks[C]//Advances in Neural Information Processing Systems. 2018: 2740-2749.
  4. 分布式近端原对称对偶算法
    • Hong M, Hajinezhad D, Zhao M M. Prox-PDA: The proximal primal-dual algorithm for fast distributed nonconvex optimization and learning over networks[C]//International Conference on Machine Learning. 2017: 1529-1538.
  5. 投影-free的分布式在线学习
    • Zhang W, Zhao P, Zhu W, et al. Projection-free distributed online learning in networks[C]//International Conference on Machine Learning. 2017: 4054-4062.
  6. 平行倒推
    • Huo Z, Gu B, Yang Q, et al. Decoupled parallel backpropagation with convergence guarantee[J]. arXiv preprint arXiv:1804.10574, 2018.
压缩通信学习

  1. 稀疏化模型

    • Wang J, Kolar M, Srebro N, et al. Efficient distributed learning with sparsity[C]//International Conference on Machine Learning. 2017: 3636-3645.

  2. 梯度量化

    • Shen Z, Mokhtari A, Zhou T, et al. Towards more efficient stochastic decentralized learning: Faster convergence and sparse communication[J]. arXiv preprint arXiv:1805.09969, 2018.

    QSGD

    • Alistarh D, Grubic D, Li J, et al. QSGD: Communication-efficient SGD via gradient quantization and encoding[C]//Advances in Neural Information Processing Systems. 2017: 1709-1720.

    PCA压缩

    • Garber D, Shamir O, Srebro N. Communication-efficient algorithms for distributed stochastic principal component analysis[J]. arXiv preprint arXiv:1702.08169, 2017.

    \(1Bits\)量化

    • Seide F, Fu H, Droppo J, et al. 1-bit stochastic gradient descent and its application to data-parallel distributed training of speech dnns[C]//Fifteenth Annual Conference of the International Speech Communication Association. 2014.
    • Wen W, Xu C, Yan F, et al. Terngrad: Ternary gradients to reduce communication in distributed deep learning[C]//Advances in neural information processing systems. 2017: 1509-1519.
错误补偿压缩
\(1Bits\)量化
  • Seide F, Fu H, Droppo J, et al. 1-bit stochastic gradient descent and its application to data-parallel distributed training of speech dnns[C]//Fifteenth Annual Conference of the International Speech Communication Association. 2014.
二次优化
  • Wu J, Huang W, Huang J, et al. Error compensated quantized SGD and its applications to large-scale distributed optimization[J]. arXiv preprint arXiv:1806.08054, 2018.
SignSGD
  • Bernstein J, Wang Y X, Azizzadenesheli K, et al. signSGD: Compressed optimisation for non-convex problems[J]. arXiv preprint arXiv:1802.04434, 2018.
  • Alistarh D, Hoefler T, Johansson M, et al. The convergence of sparsified gradient methods[C]//Advances in Neural Information Processing Systems. 2018: 5973-5983.

算法介绍

算法描述

本文采用参数服务器架构描述该算法，但是算法的应用场景不仅限于参数服务器架构，在第\(t\)次迭代，我们将该算法的关键步骤描述如下：

  • 工作节点计算

每个节点\(i\)计算本地随机梯度\(\nabla F\left(\boldsymbol{x}_{t} ; \boldsymbol{\zeta}_{t}^{(i)}\right)\)，该梯度基于全局模型\(x_t\)以及本地样本\(\boldsymbol{\zeta}_{t}^{(i)}\)。这里的\(i\)代表工作节点\(i\)的索引，\(t\)表示本轮的迭代次数

  • 工作节点压缩

每个工作节点\(i\)计算误差补偿随机梯度 \[ \boldsymbol{\delta}_{t}^{(i)}=\boldsymbol{v}_{t}^{(i)}-Q_{\omega_{t}^{(i)}}\left[\boldsymbol{v}_{t}^{(i)}\right] \] 其中\(Q_{\omega_{t}^{(i)}}\left[\boldsymbol{v}_{t}^{(i)}\right]\)表示压缩误差补偿随机梯度

  • 参数服务器压缩

所有节点将计算所得的\(Q_{\omega_{t}^{(i)}}\left[\boldsymbol{v}_{t}^{(i)}\right]\)量化梯度发送给参数服务器，参数服务器聚合所有量化梯度\(Q_{\omega_{t}^{(i)}}\left[\boldsymbol{v}_{t}^{(i)}\right]\)，并且更新全局误差补偿随机梯度\(v_t\)，根据以下式子对梯度误差\(\boldsymbol{\delta}_{t}\)进行更新 \[ \begin{array}{l} \boldsymbol{v}_{t}=\boldsymbol{\delta}_{t-1}+\frac{1}{n} \sum_{i=1}^{n} Q_{\omega_{t}^{(i)}}\left[\boldsymbol{v}_{t}^{(i)}\right] \\ \boldsymbol{\delta}_{t}=\boldsymbol{v}_{t}-Q_{\omega_{t}}\left[\boldsymbol{v}_{t}\right] \end{array} \]

  • 工作节点更新

参数服务器将\(Q_{\omega_{t}^{(i)}}\left[\boldsymbol{v}_{t}^{(i)}\right]\)发送给所有工作节点，所有工作节点更新本地模型： \[ \boldsymbol{x}_{t+1}=\boldsymbol{x}_{t}-\gamma Q_{\omega_{t}}\left[\boldsymbol{v}_{t}\right] \] 其中\(\gamma\)表示学习率

压缩选择

该方法不像当前存在的方法，并不需要无偏压缩的限制（也就是\(\mathbb{E}_{\omega} Q_{\omega}[\boldsymbol{x}]=\boldsymbol{x}\)）。所以选择压缩的方法是非常灵活的。论文例举了多种较为常用的压缩选项：

随机量化

对于任意真实值\(z \in[a, b]\)，其中\((a,b)\)是定义好的低bit数值，\(z\)会有\(\frac{b-z}{b-a}\)的概率被压缩到\(a\),有\(\frac{z-a}{b-a}\)的概率压缩到\(b\)。这种压缩操作是无偏的。

\(1Bits\)量化

将\(x\)向量压缩到\(\|x\| \operatorname{sign}(x)\)，其中\(sign(x)\)是其中\(x\)向量对应元素的符号。这种压缩是有偏的

Clipping

对于真实值\(z\)，直接设置低于\(k\)bis的部分压缩到\(0\)。例如，将\(1.23456\)压缩为d\(1.2\)，直接将其较低的四位变成\(0\)。这种压缩是有偏的。

Top-k稀疏化

对于向量\(x\)，将其最大的\(k\)个元素进行保留，其余的设置为\(0\)。这种操作是有偏的。

随机稀疏化

对于真实值\(z\)，有\(p\)的概率将\(z\)设置为\(0\)，以及\(p\)的概率设置为\(z/p\)。这样的方法是无偏的

数学证明和收敛性分析

待补充...

实验

实验设置

数据集和模型

  • ResNet-18以及CIFAR-10

实现对照组

DOUBLESQUEEZE
\(1-bit\)压缩

将梯度压缩到\(1-bit\)，只包含符号。基于向量考虑，它的比例因子表示为： \[ \frac{\text { magnitude of compensated gradient }}{\text { magnitude of quantized gradient }} \]

Top-k压缩
QSGD

工作节点将梯度压缩成三元表示，其中每个元素用\(\{-1,0,1\}\)表示。假设在这个梯度向量各个元素中的最大绝对值为\(m\)，对于任意一个元素\(e\)，它都以\(|e| /|m|\)的可能性压缩到\(sign(e)\)，以\(1-|e| /|m|\)的可能性压缩到\(0\)。扩展因子可以记为： \[ \frac{\text { magnitude of compensated gradient }}{\text { magnitude of quantized gradient }} \] 采用这种方法时，参数服务器将梯度分发的时候不会讲梯度再次压缩

Vanilla SGD

并不采用任何压缩处理

MEM-SGD

和DEOUBLESQUEEZE的区别是从参数服务器进行分发的梯度不进行压缩，对于此种方法，本文也去使用了\(1-bit\)二和\(top-k\)这两中压缩方法。

Top-k SGD

该方法不涉及误差补偿机制

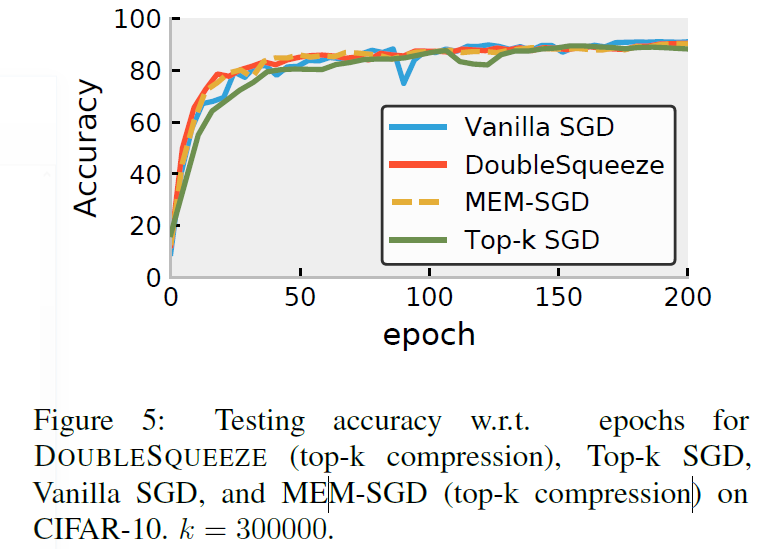
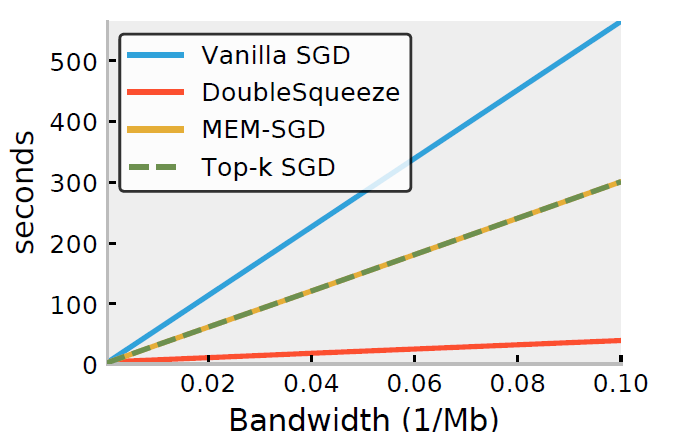
实验结果

  1. 将\(1-bit\)压缩作为DEUBLESQUEEZE的压缩方法，与MEM-SGD, QSGD这些压缩方法做对比

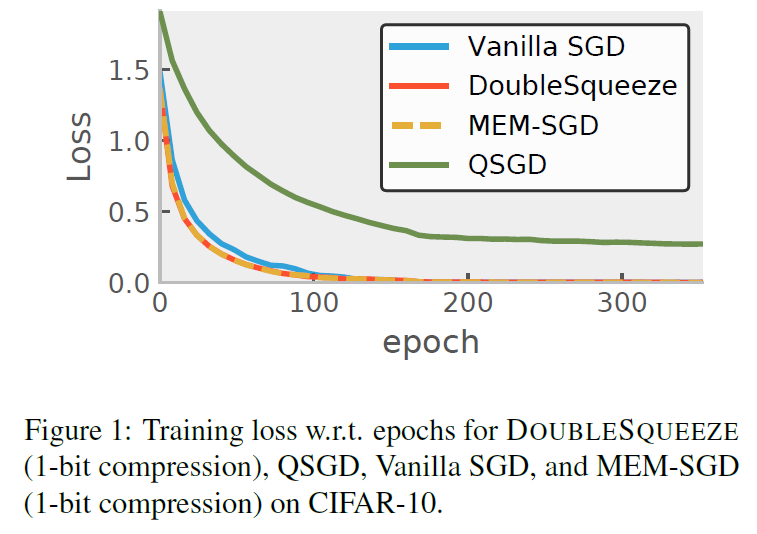
image-20200724191830893

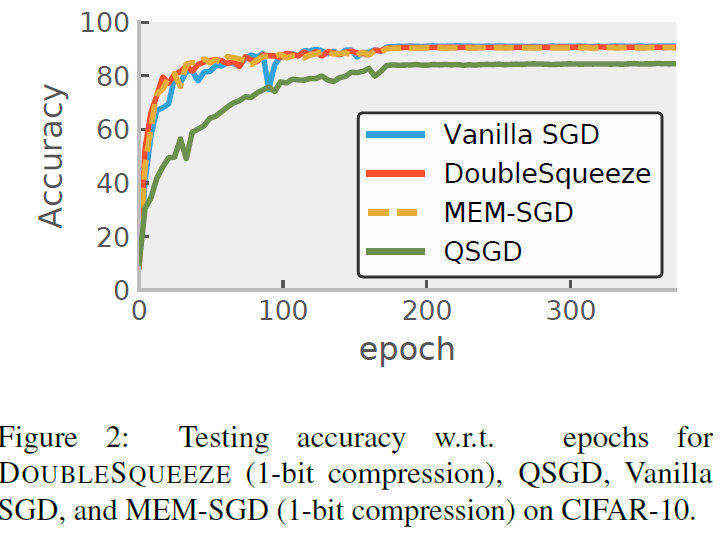
image-20200724192014337

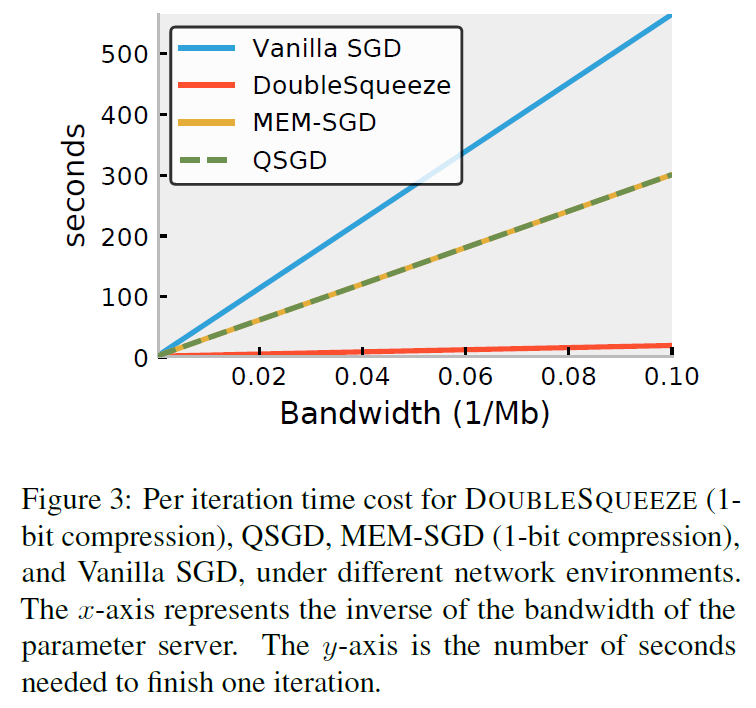
image-20200724192043966

  1. 将Top-k压缩作为DEUBLESQUEEZE的压缩方法，与MEM-SGD, QSGD这些压缩方法做对比

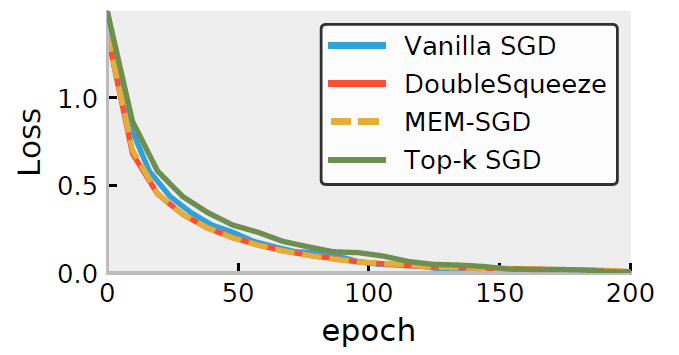
image-20200724192139291

image-20200724192150444

image-20200724192202959

相关文章推荐